Empty Space - 解金字塔魔方

不懂魔方。本文推出的方法可能很慢很蠢，实测速度还不如暴力。不过毕竟是自己推出来的，还是记录一下。

班长来串寝，带来两个魔方，跟我另一个玩魔方的舍友讨论得热烈。他们给了我一个「简单」的三阶金字塔，并说「你拼好一个面他就还原了，拼不好就再拼，总是会还原的」。

我的魔方水平限于三阶还原一个面，听他们这么说便尝试了一下，结果费了好大劲才拼出一个面。但慢慢我找到一点技巧，算是摸到了三阶金字塔的门槛。

定义

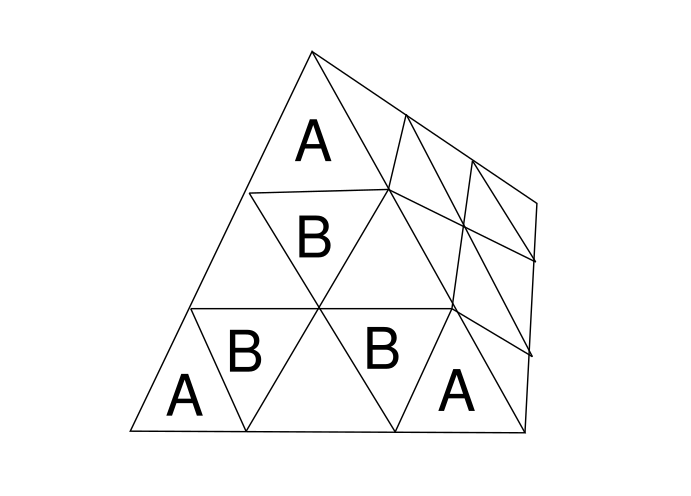
首先定义三种块：

有三个面的为角块（A）
有两个面的为棱块（B）
只有一个面的为中心块（C）

简单的预处理

当晚，我得到一个「准基本操作」，还原一个面：

把角块（A）还原（找到有相同颜色面的三个角，把同色的面转到一个平面上）
把中心块（B）还原（中心块是和角块相邻的块，一开始我甚至不知道这点）（转动角块下面的那一层，相邻的中心块还原）
把其余的棱块凑上去

到这个时候，还原其他三个面的角块和中心块是分分钟的事情了。

将上面两步结合起来，就得到了「预处理」操作：

还原所有角块和中心块
还原一个面
把还原好的面变成底面

预处理后，我们称红色中心块和角块所在的面为「红面」，其他面以此类推。

其实预处理之后，暴力破解已经很容易了。不过我不满足于此，因为我不知道为什么能还原……经常是转着转着莫名其妙就还原了。到了第二天的操作系统课我还是在乱转。

预处理后还有什么需要还原？

回去后我发现，预处理后就只剩下棱块的排列和方向的问题了。

排列问题的解决

所谓「排列问题」，指两个棱块位置互换了，比如红蓝交界的棱块和红绿交界的棱块互换位置；所谓「方向问题」，指棱块的位置对了，但方向不对，比如，红蓝棱块位于红蓝面交界上，但是棱块的红面在魔方的蓝面上，棱块的蓝面在魔方的红面上。

我发现不可能出现只有一个棱块方向错误的情况（不过我没有证明）。解决了棱块的排列问题和方向问题，金字塔魔方的还原就解决了。

然而怎么解决这几个问题呢？我起初毫无头绪，只是在瞎转魔方找感觉，感觉得找到几个基本操作才行。一开始我找的基本操作是「转顶部角块」、「顶部角块和其下层」、「翻转整个魔方，换一个面做正面」。然而这几个操作太过于基本，虽然确实可以构成所有操作，但是对于实践没有什么指导意义，用这几个基本操作来思考，可以说是寸步难行，试了一个小时都没有头绪。不过过程中我发现了解决方向问题的一个方法，下面再表述。

四个基本操作

后来我观察我还原一个面的过程，发现有一个操作至关重要，这个操作可以使一个面的三个棱块互换。这个操作我起初只知道怎么做，但不知道应该怎么表述（用上面那三个基本操作来表述就太过繁琐了）。大概是一个面转一下，接过另一个面的棱块，再转回去。后来我发现用角块和其相邻层的旋转作为基本操作比较简便。四个基本操作定义如下图。

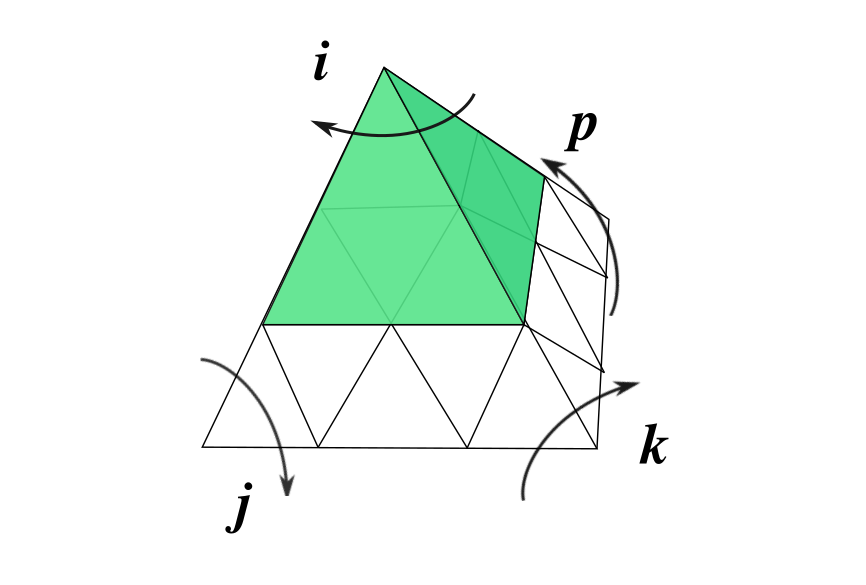
从四个基本操作出发，可以很好地表述四种面上的三轮换。起初我只找到了下面的 $\alpha$ ，并绞尽脑汁想 $\alpha$ 怎么用，但是都徒劳。直到我用纸笔描述了一下，顺藤摸瓜找到其他三个。我称下面为四个「面三轮换」操作。

$\alpha = p^{-1}kpk^{-1}$ ，效果是右面的三个棱块顺时针轮换（从右往左看）
$\beta = p^{-1}ipi^{-1}$ ，效果是左面的三个棱块逆时针轮换（从左往右看）
$\gamma = i^{-1}kik^{-1}$ ，效果是正面的三个棱块逆时针轮换（从前往后看）
$\delta = p^{-1}jpj^{-1}$ ，效果是底面三个棱块逆时针轮换（从下往上看）

对棱块进行命名和编号，如图。

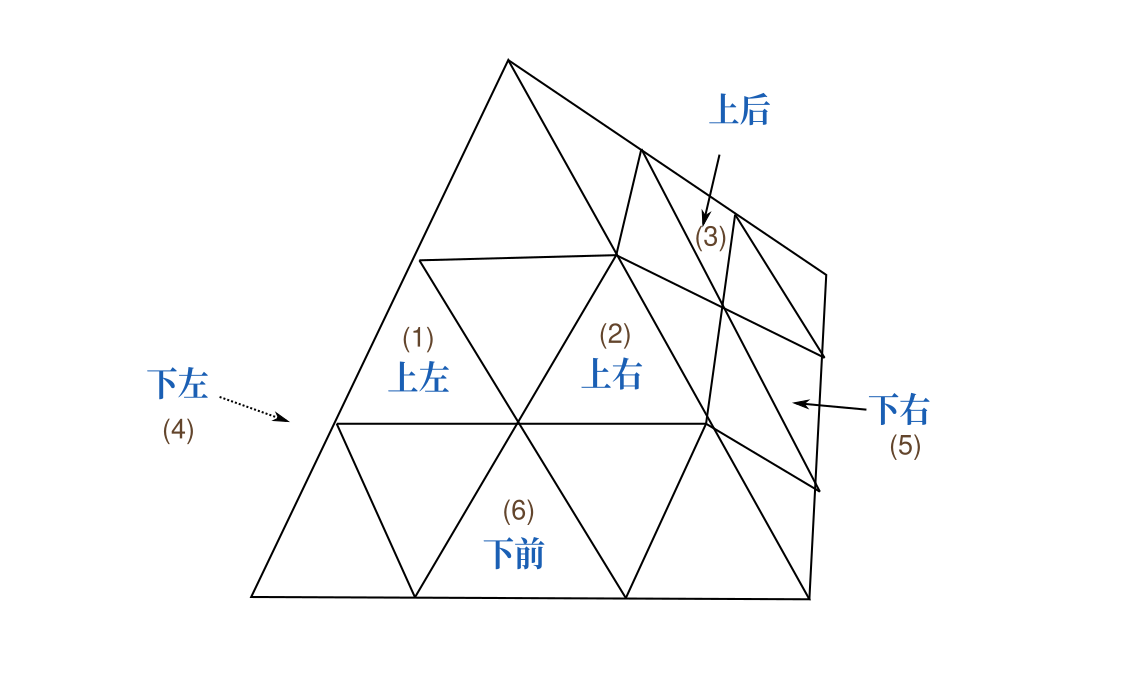
上左、上右、上后、下左、下右、下前分别标为1到6。于是四种操作的效果如下图。

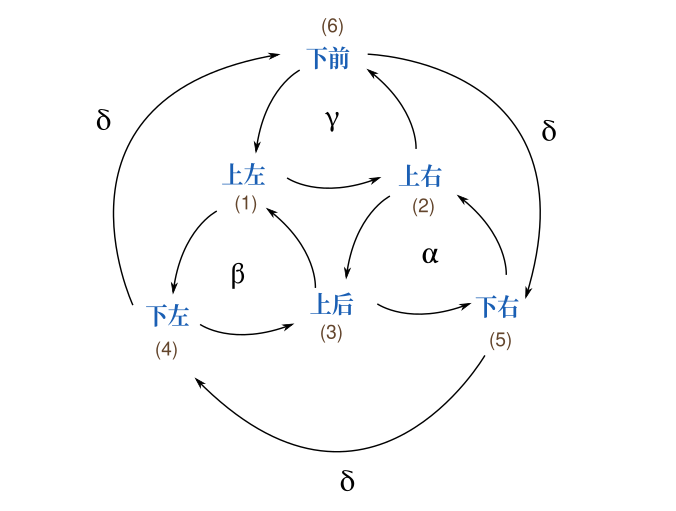
根据排列的知识和上面的标号，我发现排列问题已经被解决了。当我们完成预处理后，实际上只剩三个上棱块需要还原，由于只有三个棱块，因此，无非只有三种情况：

三个块位置都正确
三个块位置都不正确（轮换）
一个块位置正确，另外两个块互换

对于2、3情况，如果情况是可还原的，就一定可以利用几个面三轮换操作还原。如果以排列的方式表述这个问题，无非如下：

利用排列，可表述四个面三轮换。

$\alpha = \begin{pmatrix}1 & 2 & 3 &4 & 5 & 6 \\ 1 & 5 & 2 & 4 & 3 & 6\end{pmatrix}$

$\beta = \begin{pmatrix}1 & 2 & 3 &4 & 5 & 6 \\ 3 & 1 & 4 & 1 & 5 & 6\end{pmatrix}$

$\gamma = \begin{pmatrix}1 & 2 & 3 &4 & 5 & 6 \\ 6 & 1 & 3 & 4 & 5 & 2\end{pmatrix}$

$\delta = \begin{pmatrix}1 & 2 & 3 &4 & 5 & 6 \\ 1 & 2 & 3 & 4 & 5 & 6\end{pmatrix}$

对于情况2，我们只需用上面四者合成 $\omega$ 即可，称 $\omega$ 为「角三轮换」：

$\omega = \begin{pmatrix}1 & 2 & 3 &4 & 5 & 6 \\ 2 & 3 & 1 & 4 & 5 & 6\end{pmatrix}$

对于情况3，我们只需用上面四者合成 $\sigma$ 即可，称 $\sigma$ 为「棱块对换」：

$\sigma = \begin{pmatrix}1 & 2 & 3 &4 & 5 & 6 \\ 2 & 1 & 3 & 4 & 5 & 6\end{pmatrix}$

求解推公式

那么如何求解呢？我选择使用程序枚举。

程序如下：

#include <iostream>
#include <map>
#include <set>
#include <utility>
#include <string>

using namespace std;

void print_arr(int arr[6]) {
    for(int i = 0;i < 6;++i) {
        cout << arr[i] << " ";
    }
    cout << endl;
}

struct Arrangement {
    Arrangement(const initializer_list<int> l, string name = "") : name(name) {
        int i = 0;
        for(auto item : l) {
            arrange[i] = item - 1;
            ++i;
        }
    }
    Arrangement(const Arrangement &arr) : name(arr.name) {
        for(int i = 0;i < 6;++i) {
            arrange[i] = arr.arrange[i];
        }
    }
    Arrangement(int arr[6], string name = "") : name(name) {
        for(int i = 0;i < 6;++i) {
            arrange[i] = arr[i];
        }
    }
    int arrange[6];
    std::string name;
    void apply(int array[6]) const {
        int temp[6];
        for(int i = 0;i < 6;++i) {
            temp[arrange[i]] = array[i];
        }
        for(int i = 0;i < 6;++i) {
            array[i] = temp[i];
        }
    }
    void print() const {
        cout << "Arrangement " << name << " : (" << endl;
        int temp[6] = {1, 2, 3, 4, 5, 6};
        print_arr(temp);
        apply(temp);
        print_arr(temp);
        cout << ")" << endl;
    }
    bool operator<(const Arrangement &b) const {
        for(int i = 0;i < 6;++i) {
            if(arrange[i] < b.arrange[i]) {
                return true;
            }
            else if(arrange[i] > b.arrange[i]) {
                return false;
            }
            else {
                continue;
            }
        }
        return false;
    }
    bool operator==(const Arrangement &b) const {
        for(int i = 0;i < 6;++i) {
            if(arrange[i] != b.arrange[i]) {
                return false;
            }
        }
        return true;
    }
    Arrangement operator*(const Arrangement &b) const {
        int temp[6];
        for(int i = 0;i < 6;++i) {
            temp[i] = b.arrange[arrange[i]];
        }
        return Arrangement(temp, name + b.name);
    }
};

Arrangement alpha{1, 3, 5, 4, 2, 6}, beta{4, 2, 1, 3, 5, 6}, gamma{2, 6, 3, 4, 5, 1}, delta{1, 2, 3, 6, 4, 5};
std::set<Arrangement> s;

void enumarate_all() {
    int new_size = 0;
    while(true) {
        std::set<Arrangement> new_set;
        for(auto a : s) {
            for(auto b : s) {
                auto temp = a*b;
                if(s.find(temp) == s.end()) {
                    cout << "find new OP" << endl;
                    a.print();
                    cout << "and" << endl;
                    b.print();
                    cout << "forms" << endl;
                    temp.print();
                    cout << endl;
                    new_set.emplace(temp);
                }
            }
        }
        new_size = new_set.size();
        if(new_size == 0) {
            break;
        }
        new_size = 0;
        for(auto n : new_set) {
            s.emplace(n);
        }
    }
    cout << "total: " << s.size() << endl;
}

int main() {
    alpha.name = "α";
    beta.name = "β";
    gamma.name = "γ";
    delta.name = "δ";
    alpha.print();
    beta.print();
    gamma.print();
    delta.print();
    // (alpha * beta).print();
    s.emplace(alpha);
    s.emplace(beta);
    s.emplace(gamma);
    s.emplace(delta);
    enumarate_all();
    return 0;
}

程序会输出四个面三轮换组成的所有排列。果然，我在输出中找到了 $\omega$ 和 $\omega^{-1}$

Arrangement δαγβα : (
1 2 3 4 5 6 
2 3 1 4 5 6 
)
Arrangement δαδδγ : (
1 2 3 4 5 6 
3 1 2 4 5 6 
)

由于 $\omega^{-1}$ 看起来更简单，所以我偏爱后者。这就能够解决角三轮换的问题。不过我没有找到棱对换的排列，说明这种现象对于正确的魔方是不可能存在的，实践中确实也没有碰到。至此排列问题解决。

方向问题

关于方向问题，我发现我可以同时调换两个块的方向，操作如下，我称为「二倒向」。

$s = p^{-1}kpk^{-1}\cdot pj^{-1}p^{-1}j$

这个操作把上左和下左两个棱块的方向同时翻转。原理大概是用一次三轮换，把下右、上右、上后轮换一下，再把刚刚从底面换上来的块换回底面，不过执行的「手性」和和刚刚不同。（注意到 $\alpha$ 是轮换右面的三个块，可以有一个镜像的操作轮换左面的三个块，这里执行 $\alpha$ 后执行的操作大概是 $\delta$ 的镜像，所以说二者手性不同）。至此方向问题解决（奇数个棱块方向不同是不可能的）。

完整的方法

最后，一套方法开发出来了，经测可用。但是……不比暴力快。

预处理
若三个上棱块没有归位，那么就用「角三轮换」使之归位
所有块归位后，若存在方向问题，那么用「二倒向」使之取向正确