定义

sinh⁡x=ex−e−x2 \sinh x = \frac{e^x-e^{-x}}{2}

cosh⁡x=ex+e−x2 \cosh x = \frac {e^x + e^{-x}}{2}

考虑复变函数cos⁡x\cos x和sin⁡x\sin x沿着虚轴切开。由此可以理解一些性质

求导和积分

(sinh⁡x)′=cosh⁡x (\sinh x)' = \cosh x

(cosh⁡x)′=sinh⁡x (\cosh x)' = \sinh x

∫sinh⁡x=cosh⁡x+C \int \sinh x = \cosh x +C

∫cosh⁡x=sinh⁡x+C \int \cosh x = \sinh x + C

反函数

推导，设y=sinh⁡xy = \sinh x，那么

y=ex−e−x2⇔ 2yex=e2x−1⇔ e2x−2yex−1=0⇒ ex=2y+4y2+42=y+y2+1⇒ x=ln⁡(y2+1+y) \begin{aligned} & y = \frac{e^x-e^{-x}}{2} \\ \Leftrightarrow &\ 2ye^x = e^{2x} - 1 \\ \Leftrightarrow &\ e^{2x} - 2ye^x - 1 = 0 \\ \Rightarrow &\ e^x = \frac{2y + \sqrt{4y^2 + 4}}{2} = y + \sqrt{y^2 + 1} \\ \Rightarrow &\ x = \ln\left(\sqrt{y^2+1} + y\right) \end{aligned}

如果设y=cosh⁡xy = \cosh x，那么

y=ex+e−x2⇔ 2yex=e2x+1⇔ e2x−2yex+1=0⇒ ex=2y+4y2−42=y+y2−1⇒ x=ln⁡(y2−1+y) \begin{aligned} & y = \frac{e^x+e^{-x}}{2} \\ \Leftrightarrow &\ 2ye^x = e^{2x} + 1 \\ \Leftrightarrow &\ e^{2x} - 2ye^x + 1 = 0 \\ \Rightarrow &\ e^x = \frac{2y + \sqrt{4y^2 - 4}}{2} = y + \sqrt{y^2 - 1} \\ \Rightarrow &\ x = \ln\left(\sqrt{y^2-1} + y\right) \end{aligned}

得到反函数的表达式

sinh⁡−1x=ln⁡(x2+1+x) \sinh^{-1} x = \ln\left(\sqrt{x^2 + 1} + x\right)

cosh⁡−1=ln⁡(x2−1+x) \cosh^{-1} = \ln\left(\sqrt{x^2 - 1} + x\right)

反函数的求导

(sinh⁡−1x)′=1u2+1 (\sinh^{-1} x)' = \frac{1}{\sqrt{u^2 + 1}}

(cosh⁡−1x)′=1u2−1 (\cosh^{-1} x)' = \frac{1}{\sqrt{u^2 - 1}}

如果不知道上述两个公式，在推导上述等号右边两个函数的的积分的时候，需要用到三角换元法。设x=tan⁡θx = \tan \theta

∫1x2+1dx=∫sec⁡θdθ \int \frac{1}{\sqrt{x^2 + 1}} dx = \int \sec \theta d\theta

如果不记得sec⁡θ\sec\theta的积分，那还得接着推

∫sec⁡xdx=∫cos⁡x dxcos⁡2x=∫dsin⁡x1−sin⁡2x \int \sec x d x = \int \frac{\cos x \ dx}{\cos^2 x} = \int \frac{d \sin x}{1 - \sin^2 x}

设t=sin⁡xt = \sin x，那么

∫dt(1−t)(1+t)=∫11+tdt+∫11−tdt=12ln⁡∣1+t∣−12ln⁡∣1−t∣+C=12ln⁡∣1+t1−t∣+C \begin{aligned} & \int \frac{dt}{(1-t)(1+t)} \\ =& \int \frac{1}{1+t}dt + \int \frac{1}{1-t}dt \\ =&\frac{1}{2} \ln|1+t| - \frac{1}{2}\ln|1-t| + C \\ =& \frac{1}{2}\ln\left| \frac{1+t}{1-t} \right| + C \end{aligned}

代回去，得到

∫sec⁡x=ln⁡∣sec⁡x+tan⁡x∣+C \int \sec x = \ln | \sec x + \tan x| + C

使用这一公式，得到我们最后想要求的积分，不过代回之前需要做一些准备

∣cos⁡x∣=1tan⁡2x+1 |\cos x| = \frac{1}{\sqrt{\tan^2 x + 1}}

于是就可以代回了

∫dxx2+1=ln⁡(x2+1+x)+C \int \frac{dx}{\sqrt{x^2 + 1}} = \ln\left(\sqrt{x^2 + 1} + x\right) + C

真是大费周章。

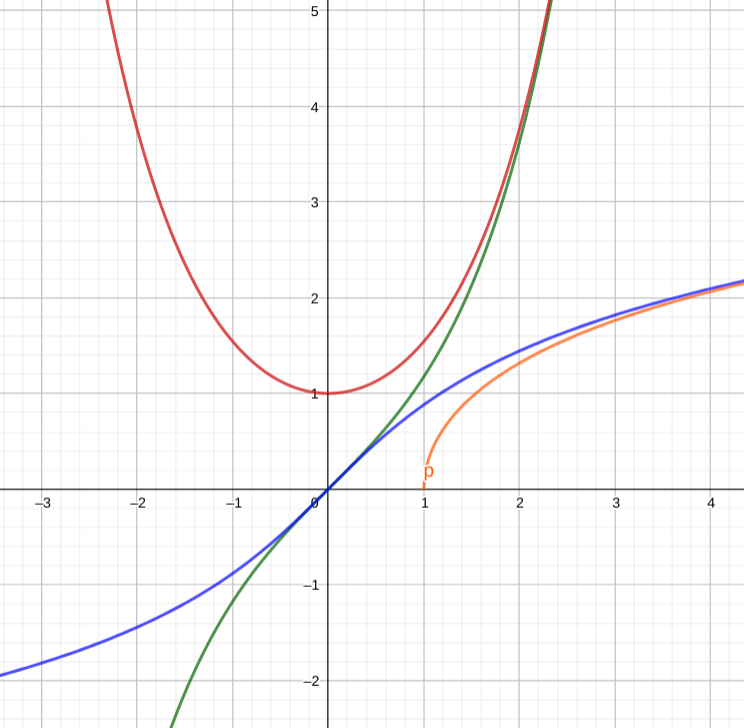
图像

猜猜哪条对应哪个函数