起因

求积分

∫dxx(1−x) \int \frac{dx}{\sqrt{x(1-x)}}

解法

解法一：答案的解法

∫dxx(1−x)=2∫dx2x⋅1−(x)2=∫d(x)1−(x)2=arcsin⁡x+C \begin{aligned} &\int \frac{dx}{\sqrt{x(1-x)}} = 2\int \frac{dx}{2\sqrt{x}\cdot\sqrt{1-(\sqrt{x})^2}} \\ = & \int \frac{d(\sqrt{x})}{\sqrt{1-(\sqrt{x})^2}} = \arcsin{\sqrt{x}} + C\\ \end{aligned}

嗯，对，没有任何毛病，t=xt=\sqrt{x}的换元也很巧妙。

解法二：我起初的解法

∫dxx−x2=∫dx14−(x2−12)=∫d(2x−1)1−(2x−1)2=arcsin⁡(2x−1)+C \begin{aligned} & \int \frac{dx}{\sqrt{x-x^2}} \\ = & \int \frac{dx}{\sqrt{\frac{1}{4} - \left(x^2-\frac{1}{2} \right)}} \\ = & \int \frac{d(2x-1)}{\sqrt{1-(2x-1)^2}} = \arcsin{(2x-1)} + C \end{aligned}

很暴力，直接配方，但是似乎也找不出毛病，积分结果和上面看起来完全不同。（因为一开始我画错了图，所以甚至以为不是同一个函数）。求导一下，发现导函数和答案得到的一样。

解法三：Wolfram Alpha的解法

∫dx1−x2=∫dx14−(12−x2)=−2∫d(1−x)1−(1−x)2=−2arcsin⁡1−x+C \begin{aligned} & \int \frac{dx}{\sqrt{1-x^2}} \\ = & \int \frac{dx}{\sqrt{\frac{1}{4} - \left(\frac{1}{2} - x^2 \right)}} \\ = & -2\int \frac{d(\sqrt{1-x})}{1 - (\sqrt{1-x})^2} \\ = & -2\arcsin{\sqrt{1-x}} + C \end{aligned}

思路诡异，但是没毛病，也许这就是机器和人的差别吧。可是凭什么说这个函数和前面两个函数是一样的？虽说求导结果一样。

函数图像

求导结果一样就意味着函数图像应该形状相同。其实也确实是相同的，用GeoGebra画出来的图如下。

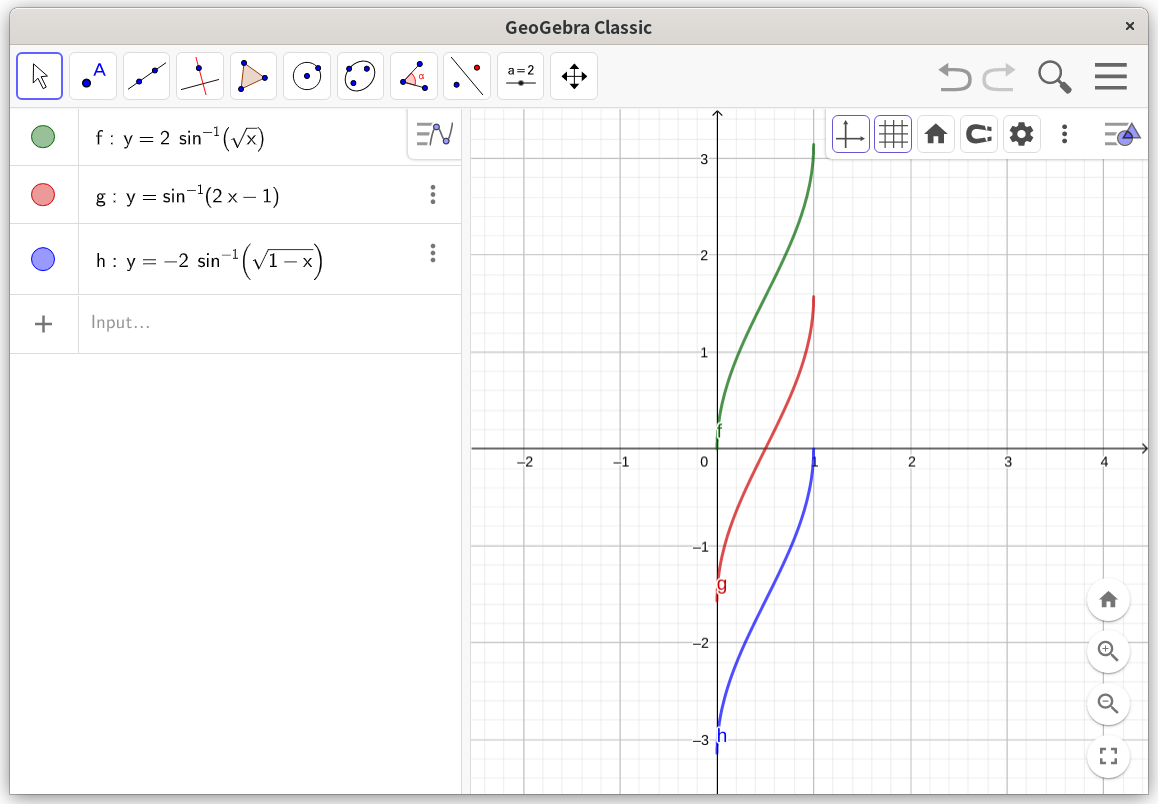
ps. 一开始我画错图了，导致我一直被图误导

证明

关于答案和wolframalpha的结果，使用对称性可破。

关于我的结果和答案，则需要使用半角公式。也就是证明2arcsin⁡x−arcsin⁡(2x−1)=C2\arcsin\sqrt{x} - \arcsin(2x-1) = C

证明：

首先，设

y1=2arcsin⁡xy2=arcsin⁡(2x−1) \begin{aligned} & y_1 = 2\arcsin\sqrt{x} \\ & y_2 = \arcsin(2x-1) \end{aligned}

那么有

x=sin⁡2y12=1+sin⁡y22 x = \sin^2\frac{y_1}{2} = \frac{1 + \sin y_2}{2}

另有

sin⁡2y12=1−cos⁡y12 \sin^2 \frac{y_1}{2} = \frac{1-\cos{y_1}}{2}

故

1−cos⁡y1=1+sin⁡y2⇔sin⁡y2=−cos⁡y1=sin⁡(y1+π2+2kπ) 1-\cos{y_1} = 1 + \sin y_2 \Leftrightarrow \sin y_2 = -\cos y_1 = \sin (y_1 + \frac{\pi}{2} + 2k\pi)

所以

y2=y1+(4k+1)π2 y_2 = y_1 + (4k+1)\frac{\pi}{2}

证毕。对于这个情况，k=−1k=-1。

总结

不仅仅涉及三角函数的积分可能没有所谓”最简“的结果，涉及反三角函数的积分可能也没有”最简“的结果，但正确结果之间肯定是相互等价的，这点大可放心。

三角函数的半角公式应用到反三角函数中，可以得到一波稀奇古怪的公式。

arcsin⁡(2x2−1)=2arcsin⁡x−π2 \arcsin(2x^2-1) = 2\arcsin x - \frac{\pi}{2}